I was recently asked by a fan of LoSpec.com how Tessellate works. I’ve been waiting for the perfect opportunity to nerd out about it so here goes!
A Bird’s Eye View
The entire simulation runs in the browser. Shapes grow outward from a root shape until they fill the screen. Each shape is just a polygon which is connected to other polygons, and I use a set of rules to determine which shapes are allowed to grow off of one another, and from which edges they’re allowed to grow.
While it’s running, the simulation tracks a list of live edges all polygons already on screen. Live edges could host a new polygon, but don’t have one yet. At each step, it checks the list of live edges, randomly picks one that’s free, and randomly picks a rule to apply (more on the rules later). Then, it pretends to place the new polygon and checks for any intersections with existing polygons or the boundary of the simulation. If it can’t find any rules to apply, it marks the edge as dead and tries to pick another.
But what are these rules and how are they applied? The answer is that they’re shape grammars, and before explaining how they work, I’m going explain a simpler kind of grammar.
Formal Grammars
You might be thinking “I hate grammar” – but trust me, this is a lot simpler – and a lot more abstract – than what you may have learned in your language class to diagram sentences.
A grammar is just a list of rules that we can use to create a valid structure out of parts. The easiest way to explain this is to use letters to form words. The “words” we’re going to form are going to be nonsense strings like ‘aaa’, or ‘aba’, but they’re a lot easier to work with than shapes, so it’s a good place to start.
Each formal grammar looks something like this.
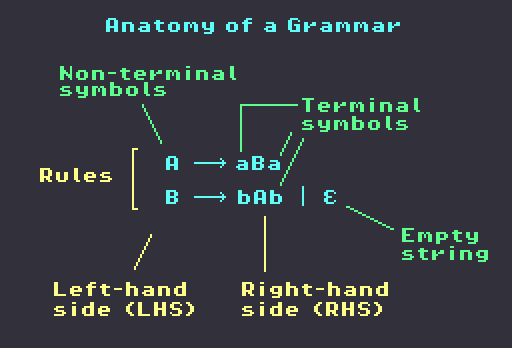
Each rule has two sides, the right-hand-side (RHS) and left-hand side (LHS), separated by an arrow. The LHS always contains at least one non-terminal symbol, which is replaced with one of the options found on the RHS. Each option is separated by a vertical bar. The ’empty string’ in the diagram is just a placeholder which means ‘replace with nothing’. Every grammar also has a starting point from which the rules are applied.
Here’s an example, using the rules above, which are repeated below. We assume the start symbol is ‘A’.
Grammar:
-> A (start at A)
A -> aBa
B -> bAb | ""
Derivation:
A (start symbol)
aBa (applied A -> aBa)
abAba (applied B -> bAb)
abaBaba (applied A -> aBa)
abaaba (applied B -> "")
final result: "abaaba"
As you can see, we can derive different sentences by applying the rules at each step. Seen this way, a grammar is a description of the rules used to generate a sequence of letters.
See? That wasn’t so bad, and it doesn’t feel anything like diagramming sentences. By the way, they’re called grammars because that’s what Noam Chomsky was studying when he invented them. Unfortunately, I haven’t been able to do his work justice in this post. Maybe someday.
Shape Grammars
The key insight behind shape grammars is we can use these rules to generate structures other than sequences of letters. Instead of letters, we can use shapes. To make this work, we need to identify how to concretely describe how shapes fit together. There are lots of ways to do this. Here’s what I do in Tesselate.
First – shapes in Tesellate only attach to one another by sharing an edge.

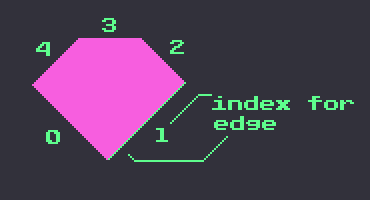
Each shape is a polygon with its edges 0-indexed with an integer, in counter-clockwise order (we chose counter-clockwise arbitrarily for consistency and sanity’s sake).
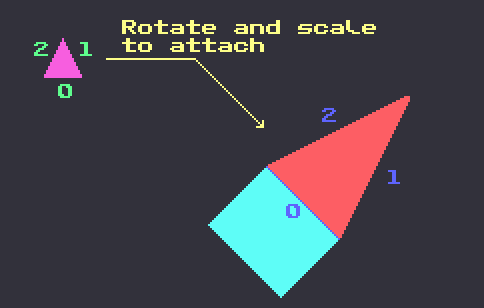
When a new shape connects to an existing shape, edge 0 of the new shape is matched up with an edge of the existing shape. The new shape is rotated and scaled so that edge 0 matches the existing edge.
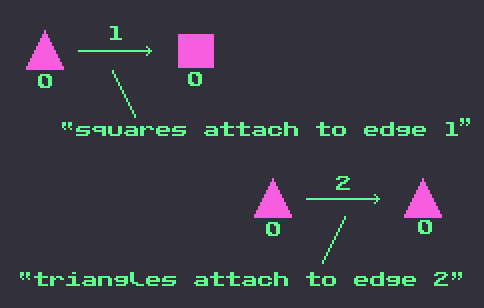
Each rule in Tesellate’s grammar explains how new shapes are allowed to attach to the edges of existing shapes in the structure. For example, you can have a triangle with edges labeled 0, 1, 2. We might write a rule saying that edge 1 can have a square attached, while edge 2 can only have another triangle attached. We might write this out as a grammer like below – making clear which edge each rule is applied to, as well as which edge is marked with index 0.
To actually run the grammar, we also need to define a start shape.
Just using this sort of structure, we can already create some really cool structures, like the one below, which was generated manually by applying the two rules above, starting from the blue triangle and alternating colors between purple and cyan at each step.

Labels
So far so good, but the rules we have at the moment don’t let us re-use shapes. What if we want to design a grammar which allows us to generate trapezoidal struts like these, one triangle at a time.

To make this happen, we’re going to need some way to distinguish between the triangles in different parts of the strut. In Tesellate, we do this by assigning a unique letter identifier to each shape, just for the purpose of making rules about it. This allows us to have different rules for different triangles in the strut.
When we apply a rule to shape, we just use its ID to lookup which rule to apply. This allows us to have further control over how the image is generated. We can have as many different shape IDs as we want, allowing us arbitrary control over the grammar.